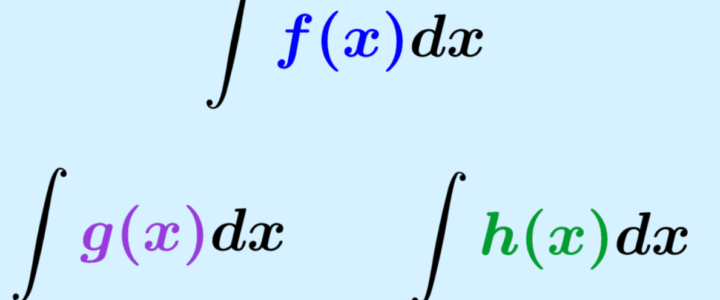
\text{Para falar de integral indefinida, falemos antes da definição de antiderivada, que é um}\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\\
 \text{conceito atrelado ao de integral.} 
\text{Sendo} \ f(x) \text{ e } F(x) \text{ definidas em } I \subset \R, \forall x \in I, \text{ dizemos que : }\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\quad\quad\qquad\quad\\
F \text{ é uma antiderivada ou uma primitiva de } f, \text{ em } I, \text{ se } F ’(x) = f(x)\\
\textbf{Exemplos:} \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\\
F(x) = x^2 \text{ é uma antiderivada (primitiva) de } f(x) = 2x, \text{ pois } F ’(x) = 2x. \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \\ 
F(x) = x^2 + 7 \text{ é uma antiderivada (primitiva) de} f(x) = 2x, \text{ pois } F ’(x) = 2x.\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\\
F(x) = x^2 + ½ \text{ é uma antiderivada (primitiva) de } f(x) = 2x, \text{ pois } F ’(x) = 2x. \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\\
F(x) = 2x \text{ é uma antiderivada (primitiva) de} f(x) = 2, \text{ pois } F ’(x) = 2. \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \\
F(x) = e^x \text{ é uma antiderivada (primitiva) de } f(x) = e^x, \text{ pois } F ’(x) = e^x. \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\\
\textbf{Definição: (Integral Indefinida)}  \text{ Se } F(x) \text{ é uma primitiva de } f(x), \text{ a expressão } F(x)+c\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \\
\text{ é chamada de integral indefinida da função }  f(x) \text{ e é denotada por:} \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\\
\int f(x) dx = F(x)+C \\
\text{A ligação que existe entre derivadas e integrais permite usar regras já 
conhecidas de de-}\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\\
\text{rivação para obter regras correspondentes para a integração. Assim, obtém-se as cha-}\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \\
\text{madas} \textit{ integrais imediatas}. \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad

\text{É possível encontrar tabelas com mais integrais imediatas e até identidades interessantes} \qquad\qquad\qquad\qquad\qquad\qquad\qquad \\
\text{nas capas de livros de cálculo.} \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \\
\textbf{Propriedades da integral indefinida} \qquad \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\\
\text{Sejam } f,g: I \to \R \text{ e } c \ne 0 \text{ uma constante. Então: }\qquad\qquad\qquad\qquad\quad \\
\text{a.} \int cf(x) dx= c\int f(x) dx \qquad\qquad\qquad\qquad\\
\text{b.} \int (f(x) \pm g(x))dx = \int f(x)dx \pm \int g(x)dx \\
\textbf{ Exercícios resolvidos } \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\\
\text{1.}\int\left(3x^2+5+\sqrt{x}\right)dx=\int 3x^2\ dx+\int 5\ dx+ \int\sqrt{x}\ dx =3\int x^2\ dx +5\int 1\ dx+\int x^{\frac{1}{2}}\ dx \qquad\qquad\qquad\qquad\qquad\qquad\qquad\\
	\qquad\qquad=\left(3. \ \frac{x^{2+1}}{2+1}+ c_1\right)+\left(5.\ x+c_2\right)+ \left(\frac{x^{1/2\ +1}}{1/2\ +1}+c_3\right)= 3\frac{x^3}{3}+5x+\frac{x^{\frac{3}{2}}}{\frac{3}{2}}+\underbrace{(c_1+c_2+c_3)}_C\\
	=x^3+5x+\frac{2\sqrt[2]{x^3}}{3}+C. \\
\text{2.} \int\left(\frac{x^3+2x+7}{x}\right)dx=\int\left(\frac{x^3}{x}+\frac{2x}{x}+\frac{7}{x}\right)dx=\int\frac{x^3}{x}\ dx+\int\frac{2x}{x}\ dx+\int\frac{7}{x}\ dx \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\\
	=\int x^2\ dx+ \int 2\ dx+\int 7\frac{1}{x}\ dx=\left(\frac{x^{2+1}}{2+1}+c_1\right)+(2x+c_2)+(7+c_3)\\
	=\frac{x^3}{3}+2x+7+\underbrace{(c_1+c_2+c_3)}_C

Se você quiser aprendar mais sobre resolução de integrais, acesse nosso canal no youtube aqui . Além disso, descubra mais coisas interessantes do mundo da matemática no nosso blog aqui.

Introdução

A matemática é uma linguagem universal que nos permite compreender e modelar fenômenos complexos. Recentemente, um grupo de pesquisadores liderado pelo Dr. Markus Tempelmayr fez uma descoberta notável no campo das equações diferenciais estocásticas. Neste post, exploraremos os detalhes dessa pesquisa e como ela pode impactar nossa compreensão de processos dinâmicos com elementos aleatórios.

Equações Diferenciais Estocásticas

As equações diferenciais estocásticas (EDEs) são ferramentas poderosas para descrever sistemas dinâmicos que envolvem incertezas. Elas aparecem em diversos contextos, desde a modelagem de crescimento bacteriano até a previsão de preços de ativos financeiros. No entanto, resolver EDEs é um desafio, especialmente quando se trata de equações parciais.

Teoria de Hairer

A pesquisa de Tempelmayr baseia-se na teoria desenvolvida pelo matemático Martin Hairer, ganhador da Medalha Fields em 2014. Hairer criou uma abordagem inovadora para resolver EDEs parciais singulares estocásticas. Essa teoria revolucionou o campo, permitindo avanços significativos na compreensão dessas equações complexas.

Abordagem Analítica

A equipe de Tempelmayr adotou uma abordagem analítica para resolver EDEs mais simples. Eles construíram soluções para equações menos complexas e, a partir delas, derivaram soluções para casos mais desafiadores. Essa estratégia é fundamental para lidar com a complexidade inerente às EDEs.

Aplicações e Impacto

Embora a pesquisa se concentre na teoria matemática, suas aplicações são amplas. Processos naturais, como a difusão de partículas em um fluido ou a propagação de ondas em meios aleatórios, podem ser modelados por EDEs. Com uma melhor compreensão dessas equações, podemos tomar decisões mais informadas em áreas como finanças, biologia e física.

Conclusão

A prova matemática desenvolvida pela equipe de Tempelmayr é um marco importante na teoria das EDEs. Ela nos aproxima de uma compreensão mais profunda dos processos dinâmicos com componentes aleatórios. À medida que continuamos a explorar o mundo através da matemática, novas descobertas como essa nos aguardam, revelando os segredos subjacentes à complexidade do universo.

Espero que este post tenha despertado seu interesse pelo mundo das equações diferenciais estocásticas. Se você quiser saber mais sobre o trabalho de Tempelmayr e sua equipe, fique à vontade para explorar as referências acadêmicas e mergulhar ainda mais fundo nesse fascinante campo! 

Mais informações: Pablo Linares et al, A diagram-free approach to the stochastic estimates in regularity structures, Inventiones mathematicae (2024). 

DOI: 10.1007/s00222-024-01275-z

Página do professor: link

Leia ainda aqui..

1. Complexidade do Conteúdo:
   • A matemática é uma disciplina intrinsecamente complexa, com conceitos abstratos e teoremas profundos. Os matemáticos enfrentam o desafio de compreender e comunicar esses tópicos de forma clara e precisa.
2. Pressão por Produtividade:
   • Na academia, há uma constante pressão para produzir pesquisas originais, publicações e projetos. Isso pode ser estressante e afetar a saúde mental dos matemáticos.
3. Competição Intensa:
   • A concorrência por bolsas de pesquisa, cargos acadêmicos e financiamento é acirrada. Os matemáticos precisam se destacar em um campo altamente competitivo.
4. Isolamento:
   • A pesquisa matemática muitas vezes envolve longas horas de trabalho solitário. Isso pode levar ao isolamento social e à falta de colaboração.
5. Falta de Reconhecimento:
   • A matemática nem sempre recebe o reconhecimento merecido. Muitos matemáticos enfrentam a sensação de que seu trabalho não é valorizado pela sociedade em geral.
6. Desafios Financeiros:
   • A carreira acadêmica pode ser financeiramente instável, especialmente para jovens pesquisadores. Salários modestos e incertezas quanto à continuidade de financiamento são comuns.
7. Equilíbrio entre Ensino e Pesquisa:
   • Professores universitários precisam equilibrar o ensino com suas atividades de pesquisa. Isso pode ser desafiador, pois ambos exigem tempo e dedicação.
8. Barreiras de Gênero e Diversidade:
   • A matemática ainda enfrenta desigualdades de gênero e falta de diversidade. Mulheres e minorias sub-representadas podem enfrentar obstáculos adicionais.
9. Exigência de Publicações:
   • Para avançar na carreira acadêmica, é necessário publicar regularmente. Isso pode ser estressante, especialmente para aqueles que preferem focar apenas na pesquisa.
10. Pressão para Inovação:
    • A matemática está sempre evoluindo. Os matemáticos enfrentam a pressão de contribuir com novas ideias e abordagens.

Apesar dessas dificuldades, muitos matemáticos são apaixonados por sua área e encontram satisfação na busca pelo conhecimento e na resolução de problemas desafiadores. A perseverança e a paixão são essenciais para superar os obstáculos e seguir uma carreira acadêmica bem-sucedida.

Introdução à Vida de Srinivasa Ramanujan

Srinivasa Ramanujan nasceu em 22 de dezembro de 1887, na pequena cidade de Erode, no estado de Tamil Nadu, Índia. Desde cedo, Ramanujan demonstrou um talento incomum para a matemática, resolvendo problemas complexos sem qualquer instrução formal. Sua infância foi marcada por uma série de dificuldades, incluindo problemas de saúde e limitações financeiras, mas isso não o impediu de seguir sua paixão.

Aos 10 anos, Ramanujan já havia superado seus colegas em matemática, e aos 16 anos, ele encontrou um livro que mudaria sua vida: “Synopsis of Elementary Results in Pure Mathematics” de G. S. Carr. Este livro, repleto de teoremas e fórmulas, serviu como um guia para suas próprias investigações matemáticas. Ramanujan começou a desenvolver suas próprias teorias e fórmulas, muitas das quais eram completamente originais e avançadas para a época.

Apesar de sua genialidade, Ramanujan enfrentou muitas dificuldades para seguir sua carreira na matemática. Ele teve problemas para se adaptar ao sistema educacional formal e, em várias ocasiões, falhou em exames de outras disciplinas devido ao seu foco exclusivo na matemática. No entanto, seu talento extraordinário começou a ser reconhecido localmente, e ele ganhou a atenção de matemáticos indianos que ficaram impressionados com suas descobertas.

Foi através de uma série de cartas enviadas ao renomado matemático britânico G. H. Hardy que Ramanujan finalmente ganhou reconhecimento internacional. Hardy ficou inicialmente cético, mas logo percebeu a profundidade e originalidade do trabalho de Ramanujan. Em 1914, com o apoio de Hardy, Ramanujan viajou para a Inglaterra, onde sua colaboração com Hardy resultou em algumas das contribuições mais significativas para a matemática do século XX.

Principais Contribuições Matemáticas de Ramanujan

Srinivasa Ramanujan é amplamente reconhecido por suas contribuições profundas e inovadoras em diversas áreas da matemática, incluindo séries infinitas, frações contínuas, teoria dos números e funções elípticas. Suas ideias frequentemente desafiavam a lógica matemática tradicional, demonstrando sua capacidade única de enxergar além dos métodos convencionais.

Uma de suas descobertas mais notáveis é a fórmula de Ramanujan para pi (π). Ramanujan desenvolveu várias séries infinitas que convergem rapidamente para π, algumas das quais foram posteriormente usadas em algoritmos modernos para calcular bilhões de dígitos de π. Sua fórmula para π é um exemplo perfeito de como suas técnicas matemáticas eram tanto elegantemente simples quanto incrivelmente poderosas.

Outro campo em que Ramanujan fez contribuições significativas é no desenvolvimento das funções theta. Estas funções são fundamentais na teoria das formas modulares e tiveram um impacto duradouro na teoria dos números e na física teórica. Suas funções theta são usadas para resolver problemas complexos e têm aplicações em áreas como a teoria das cordas e a relatividade geral.

A constante de Ramanujan é outra de suas contribuições importantes. Esta constante aparece em vários contextos matemáticos, particularmente em frações contínuas e em algumas identidades de séries. A constante ilustra a profundidade do pensamento de Ramanujan e sua habilidade para descobrir conexões inesperadas entre diferentes áreas da matemática.

Além desses exemplos, Ramanujan também é conhecido por suas contribuições à teoria dos números, onde desenvolveu teorias e fórmulas que ainda são objeto de estudo. Seus cadernos, contendo milhares de resultados matemáticos, muitos dos quais ainda não foram totalmente compreendidos, continuam a ser uma fonte rica de pesquisa para matemáticos modernos.

As ideias de Ramanujan não apenas ampliaram os horizontes da matemática, mas também desafiaram os limites do entendimento matemático da época. Suas contribuições continuam a influenciar e inspirar matemáticos, proporcionando uma base sólida para muitas das pesquisas matemáticas contemporâneas.

Colaboração com G.H. Hardy e Reconhecimento Internacional

A colaboração entre Srinivasa Ramanujan e o matemático britânico G.H. Hardy representou um marco decisivo na trajetória de Ramanujan. Em 1913, Ramanujan enviou uma carta a Hardy contendo uma série de teoremas e resultados matemáticos, muitos dos quais eram desconhecidos até mesmo pelos matemáticos mais proeminentes da época. Impressionado pela profundidade e originalidade do trabalho de Ramanujan, Hardy rapidamente reconheceu seu potencial e decidiu apoiar o prodígio indiano.

Com o apoio de Hardy, Ramanujan foi convidado a viajar para a Inglaterra em 1914 para colaborar diretamente com ele na Universidade de Cambridge. A viagem não foi isenta de desafios; Ramanujan enfrentou dificuldades significativas ao se adaptar ao clima frio e à dieta diferente, que afetaram gravemente sua saúde. Além disso, as barreiras culturais e as saudades de casa foram obstáculos constantes durante sua estada na Inglaterra.

Apesar dessas dificuldades, a parceria entre Ramanujan e Hardy rendeu frutos extraordinários. Juntos, eles publicaram uma série de artigos que expandiram significativamente o campo da teoria dos números e outras áreas da matemática. Entre suas contribuições mais notáveis estão a série de Ramanujan, a função tau de Ramanujan e o trabalho sobre frações contínuas e funções elípticas. Hardy frequentemente elogiava a intuição matemática de Ramanujan, descrevendo-o como um “gênio natural” que possuía uma capacidade inata para descobrir novos resultados matemáticos.

O trabalho de Ramanujan começou a ganhar reconhecimento internacional à medida que suas descobertas eram publicadas e discutidas na comunidade científica. Em 1918, Ramanujan foi eleito membro da Royal Society, uma das mais antigas e prestigiadas sociedades científicas do mundo. No mesmo ano, tornou-se também o primeiro indiano a ser eleito Fellow do Trinity College, Cambridge.

A colaboração com G.H. Hardy não apenas ajudou a legitimar e divulgar o trabalho de Ramanujan, mas também trouxe à tona a magnitude de seu gênio matemático, garantindo-lhe um lugar de destaque na história da matemática mundial.

Explorando Ramanujan Através do Filme “O Homem que Viu o Infinito”

‘O Homem que Viu o Infinito’, um filme baseado na biografia escrita por Robert Kanigel, fornece uma representação cinematográfica da vida do matemático indiano Srinivasa Ramanujan. Este filme é uma introdução acessível para quem deseja conhecer mais sobre as contribuições de Ramanujan à matemática. A trama segue sua jornada desde suas origens humildes em Madras, Índia, até seu trabalho inovador em Cambridge, Inglaterra, ao lado do matemático britânico G.H. Hardy.

O filme começa com a vida de Ramanujan na Índia, destacando sua paixão inata pela matemática e sua luta para encontrar reconhecimento em um ambiente acadêmico que pouco compreendia sua genialidade. A narrativa avança com a correspondência entre Ramanujan e Hardy, culminando na viagem de Ramanujan a Cambridge. A colaboração entre Ramanujan e Hardy é uma das partes centrais do filme, mostrando a dinâmica entre dois matemáticos de culturas e métodos muito diferentes.

Embora o filme tenha sido elogiado por sua fidelidade aos eventos históricos, algumas liberdades cinematográficas foram tomadas para tornar a história mais envolvente. Por exemplo, algumas situações e diálogos foram dramatizados para enfatizar os desafios enfrentados por Ramanujan. No entanto, a essência de suas descobertas matemáticas e o impacto de seu trabalho permanecem precisos, proporcionando uma visão autêntica de suas contribuições.

Como ferramenta didática, ‘O Homem que Viu o Infinito’ serve não apenas para ilustrar a vida de Ramanujan, mas também para inspirar interesse na matemática. Ele humaniza o processo de descoberta e destaca a importância da colaboração internacional e do reconhecimento intercultural no avanço do conhecimento. Ao assistir ao filme, os espectadores podem obter uma maior apreciação do impacto duradouro de Ramanujan na matemática, bem como uma compreensão das barreiras que ele superou para compartilhar seu gênio com o mundo.

Assista o Trailer:

Para saber mais sobre a vida de Ramanujan, você ainda pode acessar Aqui. Confira ainda a história e contribuição de Pitágoras clique aqui .

A Vida de Pitágoras: Origem e Formação

Pitágoras, uma figura proeminente na história da matemática, nasceu por volta de 570 a.C. na ilha de Samos, localizada na Grécia. Desde cedo, ele demonstrou uma curiosidade excepcional e uma inclinação natural para o aprendizado, o que o levou a buscar conhecimento além das fronteiras de sua terra natal.

Em sua juventude, Pitágoras viajou para o Egito, onde foi profundamente influenciado pela cultura e pelo avanço científico dos egípcios. No Egito, ele estudou sob a tutela de sacerdotes, adquirindo um vasto conhecimento em matemática, astronomia e filosofia. Essas disciplinas eram consideradas sagradas e secretas, reservadas apenas para os mais dedicados estudiosos. Pitágoras absorveu esses ensinamentos com entusiasmo, o que moldou significativamente seu pensamento e futuras contribuições.

Após sua estadia no Egito, Pitágoras continuou sua busca por sabedoria na Babilônia, outro centro de aprendizado da antiguidade. Na Babilônia, ele entrou em contato com matemáticos e astrônomos que expandiram ainda mais seu entendimento do universo. As técnicas matemáticas babilônicas, especialmente aquelas relacionadas à aritmética e geometria, foram incorporadas ao seu repertório de conhecimentos.

Ao retornar à Grécia, Pitágoras decidiu estabelecer-se em Crotona, uma colônia grega no sul da Itália. Foi lá que ele fundou a escola pitagórica, uma comunidade dedicada ao estudo da matemática, filosofia e música. A escola não era apenas um centro de aprendizado, mas também uma irmandade com regras e rituais próprios. Os pitagóricos acreditavam que os números eram a essência de todas as coisas, uma filosofia que guiou muitas de suas descobertas e teorias matemáticas.

A vida de Pitágoras foi marcada por uma busca incessante pelo conhecimento e pela verdade. Suas viagens e estudos em civilizações avançadas proporcionaram-lhe uma base sólida para suas realizações matemáticas e filosóficas, influenciando gerações de pensadores que vieram depois dele.

A Escola Pitagórica: Filosofia e Matemática

A escola pitagórica, fundada por Pitágoras no século VI a.C., não se limitava a ser um centro de estudos matemáticos; era uma comunidade que integrava aspectos religiosos, filosóficos e científicos. Os pitagóricos formavam uma irmandade secreta e rigorosamente organizada, com regras estritas que governavam a vida cotidiana de seus membros. Eles seguiam um estilo de vida ascético, abstendo-se de certos alimentos e práticas para manter a pureza do corpo e da alma. A doutrina da metempsicose, ou a crença na reencarnação, era central para suas crenças, influenciando profundamente sua ética e filosofia.

Os pitagóricos acreditavam que a essência do universo podia ser compreendida através dos números. Essa perspectiva, resumida na máxima “tudo é número”, permeava tanto suas práticas filosóficas quanto matemáticas. Para eles, os números não eram meramente ferramentas de contagem ou cálculo, mas entidades com propriedades e significados quase místicos. Acreditava-se que os números podiam explicar a harmonia e a ordem do cosmos, desde a música até as proporções geométricas. Essa visão numérica do mundo levou a diversas descobertas matemáticas significativas, incluindo a famosa relação pitagórica dos triângulos retângulos, conhecida como o Teorema de Pitágoras.

A escola pitagórica também se diferenciava por sua abordagem interdisciplinar. A matemática era vista como uma linguagem universal que podia ser aplicada para entender fenômenos naturais, filosóficos e espirituais. Os pitagóricos exploraram relações numéricas em várias áreas do conhecimento, desde a música, onde identificaram relações harmônicas baseadas em proporções numéricas, até a astronomia, onde buscaram padrões e regularidades no movimento dos corpos celestes. A crença na perfeição dos números levou-os a descobrir a existência dos números irracionais, um conceito que desafiava a ideia de que todos os números podiam ser expressos como razões de inteiros, ampliando assim os horizontes da matemática.

Assim, a escola pitagórica serviu como um elo fundamental entre a filosofia e a matemática, mostrando que a busca pelo conhecimento podia ser uma jornada integrada e holística. Essa abordagem influenciou profundamente o desenvolvimento da matemática e da ciência ocidental, deixando um legado que perdura até hoje.

Teorema de Pitágoras: A Descoberta e Suas Aplicações

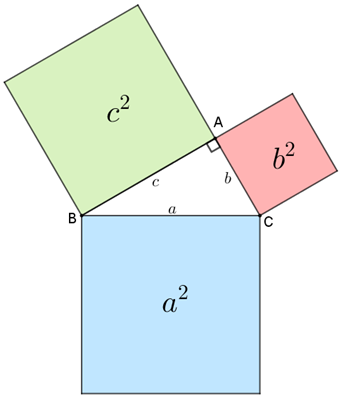
O Teorema de Pitágoras é uma das descobertas mais notáveis e influentes na história da matemática. Formalmente, o teorema afirma que, em um triângulo retângulo, o quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos outros dois lados. Matematicamente, isso é expresso pela equação: c² = a² + b², onde c representa a hipotenusa e a e b são os catetos do triângulo.

A descoberta do Teorema de Pitágoras é frequentemente atribuída ao matemático e filósofo grego Pitágoras, embora existam evidências de que princípios semelhantes eram conhecidos por culturas antigas como os babilônios e os egípcios. A demonstração matemática do teorema é considerada um marco na geometria, utilizando uma série de métodos, incluindo a decomposição de áreas e a similaridade de triângulos, para provar sua validade.

As aplicações práticas do Teorema de Pitágoras são vastas e abrangem múltiplas disciplinas. Na construção civil, o teorema é utilizado para garantir a precisão de ângulos retos e a estabilidade estrutural de edificações. Na navegação, ele auxilia na determinação de distâncias entre pontos, crucial para a cartografia e a elaboração de mapas precisos. A astronomia também se beneficia do teorema, especialmente na medição de distâncias interestelares e na análise de trajetórias de corpos celestes.

Além disso, o Teorema de Pitágoras é frequentemente empregado na resolução de problemas do cotidiano. Um exemplo clássico é determinar a distância direta entre dois pontos em um plano, como calcular a distância percorrida por uma pessoa que caminha de um ponto A a um ponto B em direções perpendiculares. Outro exemplo é no campo da física, onde o teorema é utilizado para calcular a resultante de forças perpendiculares.

Em resumo, o Teorema de Pitágoras não só representa um avanço teórico significativo, mas também uma ferramenta prática indispensável que continua a ser aplicada em diversas áreas do conhecimento humano. Sua simplicidade e utilidade exemplificam a beleza e a importância da matemática na compreensão e na interação com o mundo ao nosso redor.

Além do famoso Teorema de Pitágoras, Pitágoras e seus seguidores, conhecidos como pitagóricos, fizeram várias outras contribuições significativas para a matemática. Uma dessas contribuições foi o estudo dos números irracionais. Os pitagóricos descobriram que a raiz quadrada de 2 não podia ser expressa como uma fração de dois números inteiros, o que desafiou a crença grega de que todos os números eram racionais. Essa descoberta abriu caminho para a compreensão mais profunda dos números e suas propriedades.

Outra área de interesse dos pitagóricos foi a teoria dos números perfeitos. Um número perfeito é um número inteiro positivo que é igual à soma de seus divisores próprios. Por exemplo, o número 6 é perfeito porque 1, 2 e 3 são seus divisores próprios, e 1 + 2 + 3 = 6. Os pitagóricos também se interessaram pelos números amigos, que são pares de números em que cada número é a soma dos divisores próprios do outro. Essas investigações contribuíram significativamente para o desenvolvimento da teoria dos números.

Os pitagóricos também fizeram avanços importantes na música, descobrindo as relações harmônicas que fundamentam a teoria musical ocidental. Eles perceberam que as notas musicais podiam ser descritas matematicamente através de proporções simples entre os comprimentos das cordas vibrantes. Esse insight levou ao desenvolvimento da escala pitagórica, que ainda influencia a música moderna.

O impacto das ideias pitagóricas se estendeu muito além da matemática e da música. Platão, por exemplo, foi fortemente influenciado pelas ideias de Pitágoras sobre a harmonia e a proporção, o que se refletiu em sua própria filosofia. Euclides, outro gigante da matemática antiga, também foi influenciado pelos pitagóricos, especialmente em seu trabalho “Os Elementos”, onde muitos conceitos pitagóricos são explorados e formalizados.

O legado de Pitágoras e de seus seguidores continua a reverberar através dos séculos, afetando não apenas a matemática, mas também a ciência, a filosofia e as artes. Suas descobertas e ideias estabeleceram as bases para muitos dos avanços subsequentes nesses campos, demonstrando a interconexão entre diferentes áreas do conhecimento e a importância de uma abordagem holística para a compreensão do mundo.

Acompanhe nosso canal no youtube (4) matematicapz – YouTube e Histórias Matemáticas Que Você Não Aprend – matematicapz .